Goal
- 힙(heap)에 대한 이해
- 힙의 특징을 이해하고, 어떤 상황에서 쓰면 좋은지 설명할 수 있다.
- 힙을 표현할 수 있다
- 힙을 사용해서 우선 순위 큐를 구현하고 정렬할 수 있다.
힙(heap)이란?
완전이진트리(complete binary tree)를 기본으로 한 자료구조로서 다음과 같은 힙 속성(heap property)을 만족한다.
힙 속성(heap property)
- heap order property : 부모 자식 노드간에 대소 비교가 가능하다
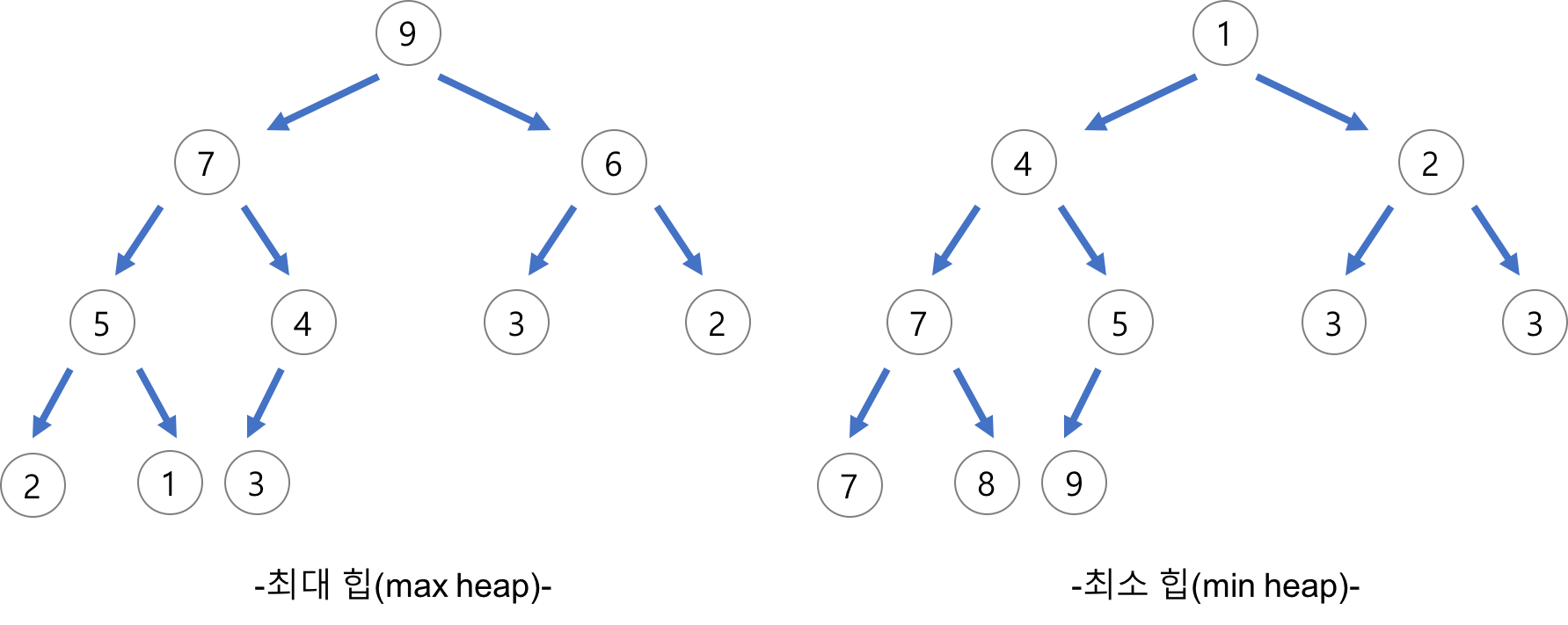
- 각 노드의 값은 자신의 자식노드가 가진 값보다 크거나 같다(최대 힙, Max heap)
- 각 노드의 값은 자신의 자식노드가 가진 값보다 작거나 같다(최소 힙, Min heap).
- heap shape property : 완전이진트리 모양이다. (완전이진트리 속성을 만족)
힙의 종류로 최대 힙(max heap)과 최소 힙(min heap)이 있다.
- 최대 힙(max heap)
- 부모 노드의 키값이 자식 노드의 키값보다 항상 크거나 같다.
- key(A) >= key(B)
- 최소 힙(min heap)
- 부모 노드의 키값이 자식 노드의 키값보다 항상 작거나 같다.
- key(A) <= key(B)
위와 같은 힙의 특징 때문에 루트 노드는 항상 최대 값(max heap일 때) 또는 최소 값(min heap일 때)만을 갖는다.
(중복 값을 허용함에 유의)
키값의 대소관계는 오로지 부모노드와 자식노드 간에만 성립하며, 특히 형제 사이에는 대소관계가 정해지지 않는다.
힙의 사용 용도
따라서, 힙은 여러개의 값들 중에서 가장 큰 값이나 가장 작은 값을 찾을 때 사용된다.
보통, 우선순위 큐(priority queue)를 구현할 때 가장 효율적인 자료구조가 heap이라서 priority queue와 heap을 동일하게 표현하는 경우가 있다. (우선 순위가 가장 높은 것이 항상 루트 노드로 오게 되어 있는 구조이다)
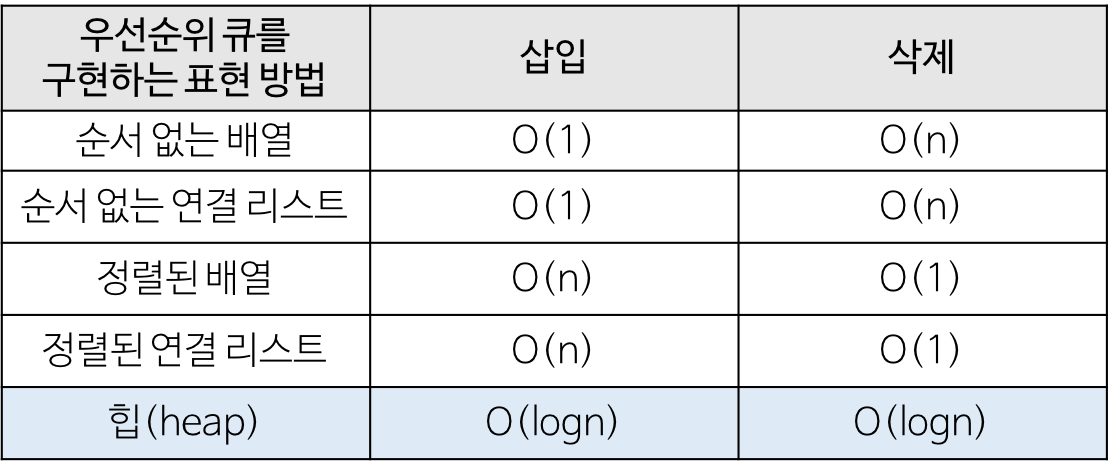
heap에 모든 데이터를 삽입하고 삭제하면 우선순위에 따라 순서대로 정렬이된다. (힙정렬)
시간 복잡도 : nlogn (삽입 : nlogn , 삭제 : nlogn)
참고) 사용 예시
- 우선순위 큐
- 힙정렬
- A-Star, 다익스트라 최단 거리 알고리즘
- Prim의 최소 스패닝 트리 알고리즘
이진 힙(binary heap)
각 노드의 자식노드의 최대개수는 힙의 종류에 따라 다르지만, 대부분의 경우는 자식노드의 개수가 최대 2개인 이진 힙(binary heap)을 사용한다. 일반적으로 힙이라고 하면 완전이진트리 구조의 이진 힙을 말한다.
이진 힙의 표현
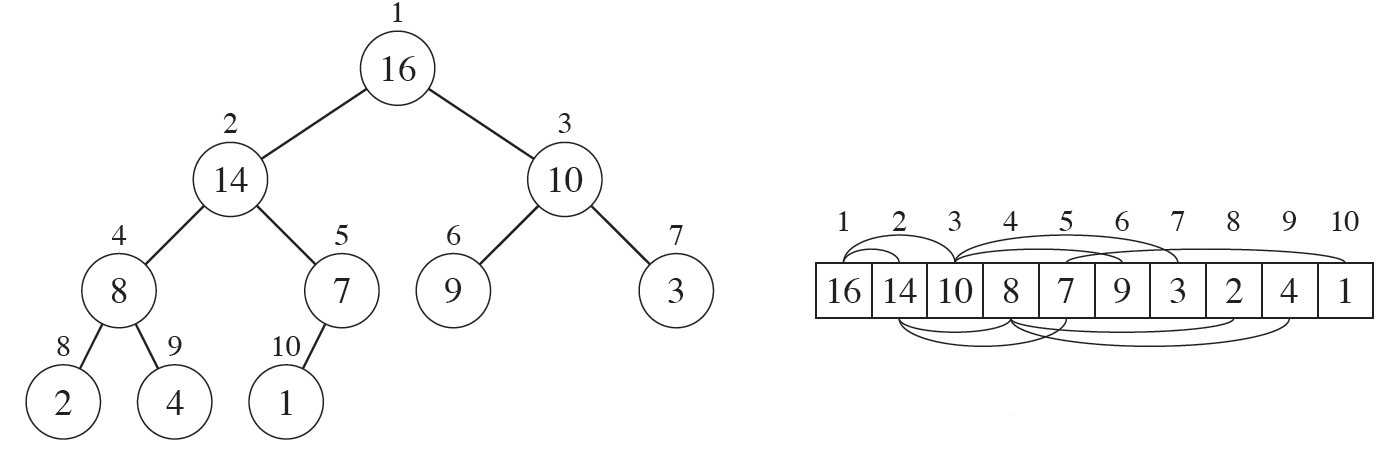
힙은 완전이진트리(complete binary tree) 성질을 만족하기 때문에 다음과 같이 1차원 배열로 자주 표현된다.
완전이진트리에서의 인덱스 표현
루트 노드 인덱스가 0인 경우 (zero-based heap)
- left-child : 2n + 1
- right-child : 2n + 2
- parent : (n-1) / 2
루트 노드 인덱스가 1인 경우 (one-based heap)
- left-child : 2n
- right-child : 2n + 1
- parent : n / 2
부모 노드 인덱스를 간단히 하기 위해 루트 노드 인덱스가 1인 경우로 자주 표현된다.
힙의 주요 연산
- 삽입(insert) : 요소 삽입
- 삭제(delete) : 루트 노드 삭제
- heapify : 트리가 힙 속성(heap property)을 만족하도록 하는 연산
- shift-up : 힙 속성(heap property)에 맞게 노드를 위로 올리는 연산. insert할 때, 에 마지막에 새 노드를 삽입하고 shift-up 한다.
- shift-down : 힙 속성에 맞게 노드를 아래로 내리는 연산. delete할 때, 루트 노드와 마지막 노드를 교환하고, 루트노드(이전 마지막 노드)를 shift-down하고 마지막 노드(이전 루트 노드)를 트리에서 제거한다.
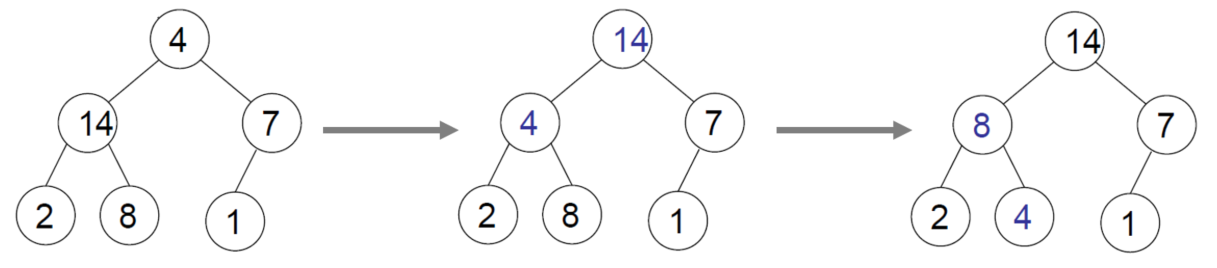
삽입, 삭제 연산에 heapify 연산이 반드시 포함 되며, 삽입, 삭제 연산이 아니더라도 기존 이진 트리를 heap으로 변경할 때 heapify연산이 사용될 수 있다.
다음 그림은 heapify 연산을 통해 기존 트리를 heap으로 변경하는 과정을 보여준다.
시간 복잡도 : O($\log_2 {n}$)
=> 최대 트리 높이(h = $\log_2 {n}$)만큼의 시간 복잡도를 가짐
다음 그림은 heap에서 삽입 연산을 하는 과정을 나타낸다.
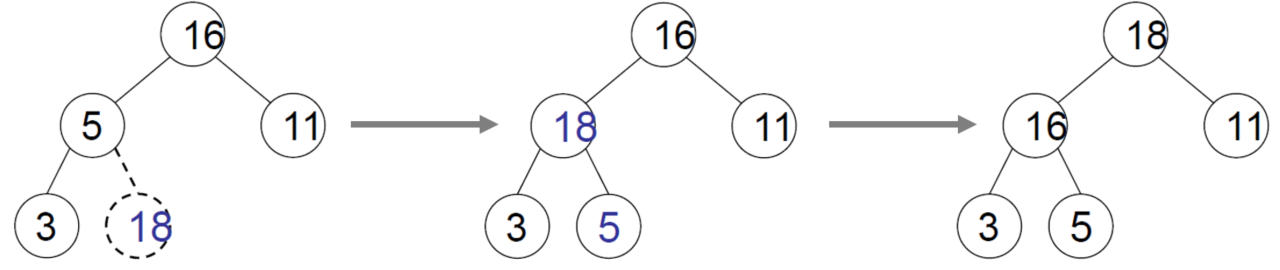
- (마지막 요소 + 1) 위치에 새 요소 삽입
- shift-up 연산
시간 복잡도 : O($\log_2 {n}$)
=> 삽입 : O(1) , shift-up : O($\log_2 {n}$) (heapify 연산이 대부분의 시간을 차지)
다음 그림은 heap에서 삭제 연산을 하는 과정을 나타낸다.
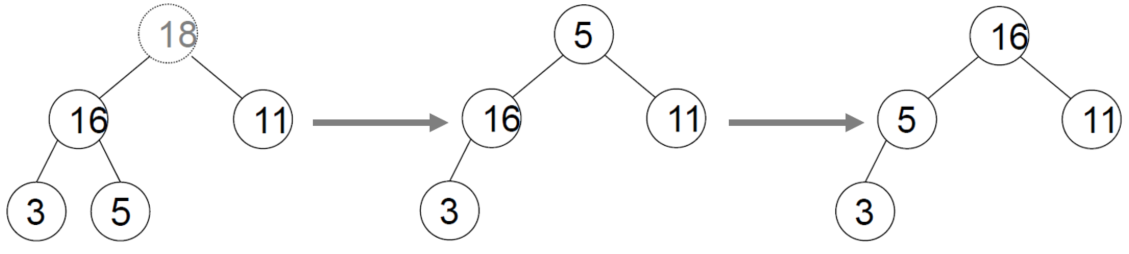
- root(18)와 마지막 노드(5)를 교환
- 루트 노드(5)에 대해서 shift-down 연산 수행
- 마지막 노드(18) 제거
시간 복잡도 : O($\log_2 {n}$)
=> 삭제 : O(1) , shift-down : O($\log_2 {n}$) (heapify 연산이 대부분의 시간을 차지)
References
heap위키 백과 참고 => 힙의 개념, 연산, 종류 등에 대해서 굉장히 자세히 설명되어 있다
https://www.quora.com/What-is-a-nearly-complete-binary-tree
https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html
https://ratsgo.github.io/data%20structure&algorithm/2017/09/27/heapsort/
'알고리즘 > 자료구조' 카테고리의 다른 글
| 해시 테이블(Hash Table) (0) | 2020.08.03 |
|---|---|
| AVL Tree (0) | 2020.07.02 |
| 가중치 그래프(Weighted Graph), 최소 신장 트리(MST) (0) | 2020.06.21 |
| 트리(Tree) (1) | 2020.06.21 |
| 그래프(Graph) (0) | 2020.06.18 |


