[BOJ 1002] 터렛

문제 : https://www.acmicpc.net/problem/1002

문제 분류 : 수학

 

원의 위치 관계를 따져보는 문제이다.

 

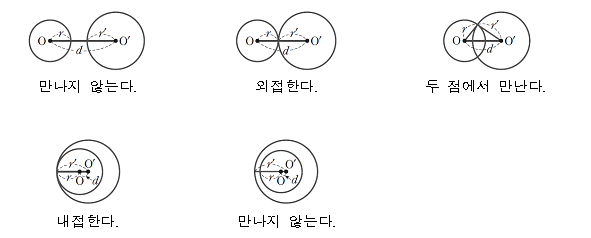
두 원의 위치 관계

1. 두 원이 일치하는 경우 => d = 0, r1 = r2
2. 만나지 않는 경우
   1) 내부에서 만나지 않는 경우 : d < |r1 - r2|  (d = 0이면 동심원)
   2) 외부에서 만나지 않는 경우 : r1 + r2 < d
3. 한 점에서 만나는 경우
   1. d = r1 + r2 (외접)
   2. d = |r1 - r2| (내접)
4.  두 점에서 만나는 경우
   1. |r1 - r2| < d < r1 + r2 => 차 < d < 합

case별로 구분했을 때, 0, 1, 2 또는 무한개의 접점이 존재하는데, 완전히 일치하는 경우를 제외 하고 유한개의 접점을 가질 때에는 내접 또는 외접을 기준으로 접점 개수가 달라진다.

 

즉, 한 점에서 만나는 경우인,

d = r1 + r2 (외접)

d = |r1 - r2| (내접)

위 두 등식을 기준으로 0, 1, 2 접점 갯수가 달라진다.

 

 

구현 코드

#include<cstdio>

int main()
{
	int T;
	scanf("%d", &T);

	int x1, y1, x2, y2, r1, r2;
	int D, R, r;

	/*
	두 원의 위치 관계
	1. 두 원이 일치하는 경우 => d = 0, r1 = r2
	2. 만나지 않는 경우
		1) 내부에서 만나지 않는 경우 : d < |r1 - r2|
		2) 외부에서 만나지 않는 경우 : r1 + r2 < d
	3. 한 점에서 만나는 경우
		1) d = r1 + r2 (외접)
		2) d = |r1 - r2| (내접)
	4. 두 점에서 만나는 경우
		1) |r1 - r2| < d < r1 + r2
		=> 차 < d < 합
	*/

	while (T--)
	{
		scanf("%d %d %d %d %d %d", &x1, &y1, &r1, &x2, &y2, &r2);

		if (x1 == x2 && y1 == y2 && r1 == r2)
		{
			printf("-1\n");
			continue;
		}

		D = (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
		R = (r1 + r2) * (r1 + r2);
		r = (r1 - r2) * (r1 - r2);

		if (D < r || R < D)
		{
			printf("0\n");
		}
		else if (D == r || D == R)
		{
			printf("1\n");
		}
		else
		{
			printf("2\n");
		}
	}
}

 

 

References

https://m.blog.naver.com/PostView.nhn?blogId=hwasin1357&logNo=20172057721&proxyReferer=https:%2F%2Fwww.google.co.kr%2F

https://mathbang.net/101