Prefix sum

Goal

• Prefix sum을 구현할 수 있다.

---

Prefix Sum이란?

시작 위치부터 현재 위치까지의 원소 합을 저장하는 배열이다.

부분 합(partial sum) 또는 누적 합(cumulative sum)이라고도 한다.

 

 

Prefix sum은 누적 합을 미리 구하는 전처리 과정을 통해 구간 합(range sum)을 빠르게 구할 때 사용된다.

 

*prefix sum : 0~b까지의 누적합 (반드시 첫번 째 원소를 포함하는 구간)

*range sum : a~b까지의 구간 합

 

예를 들어 누적 합을 저장한 배열을 pSum이라고 할 때,

[a, b] 구간의 합을 구하기 위해서 pSum[b] - pSum[a - 1]와 같은 연산을 해주면 O(1) 시간에 구간 합(range sum)을 구할 수 있다.

a가 0인 경우, pSum[b]가 0~b까지의 누적 합이 된다.

 

 

구현 코드

vector<int> prefix_sum(const vector<int>& a)
{
	vector<int> ret(a.size());
	ret[0] = a[0];

	for (int i = 1; i < a.size(); i++)
		ret[i] = ret[i - 1] + a[i];

	return ret;
}

int range_sum(const vector<int>& pSum, int a, int b)
{
	if (0 == a)	return pSum[b];
	return pSum[b] - pSum[a - 1];
}

 

2차원으로의 확장

 

 

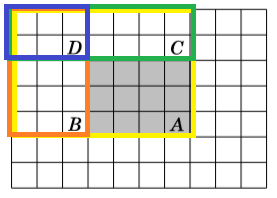
회색 부분의 구간 합을 구하고 싶을 경우 다음과 같이 구할 수 있다.

구간 합 = S(A) - S(C) - S(B) + S(D)

 

회색 영역의 왼쪽 위, 오른 쪽 아래 모서리 좌표를 각각 (r1, c1) , (r2, c2)라 할 때, 다음 식이 성립한다.

sum(r1, c1, r2, c2) = psum[r2, c2] - psum[r2, c1 - 1] - psum[r1 - 1, c2] + psum[r1 - 1, c1 - 1]

 

 

시간 복잡도

• 전처리 단계
  • 1차원 : O(N)
  • 2차원 : O(N*M)
• 계산 : O(1)

 

관련 문제

• [BOJ 11441] 합 구하기
• [BOJ 1806] 부분합
• [BOJ 1644] 소수의 연속합
• [BOJ 2015] 수들의 합 4

 

사용처

배열의 원소 값이 자주 바뀌지 않는 상황에서 두 번 이상의 구간합 질의가 있는 경우 사용할 수 있다.

만약 원소의 값이 자주 바뀐다면 펜윅 트릭(=인덱스 트리)나 세그먼트 트리를 사용하는 것이 좋다.

 

References

구간 합 배열

 

C++ 관련 라이브러리

• std::partial_sum
• std::inclusive_scan
• std::exclusive_scan