728x90
반응형
문제 링크 : https://www.acmicpc.net/problem/3009
문제 분류 : 수학
문제 자체가 어렵진 않지만, XOR연산으로도 풀 수 있다는 걸 생각 못했다.
처음 구현한 코드
#include<cstdio>
int x, y;
int point[3][2];
int main()
{
for (int i = 0; i < 3; i++)
{
scanf("%d %d", &point[i][0], &point[i][1]);
}
point[0][0] == point[1][0] ? x = 2 : point[0][0] == point[2][0] ? x = 1 : y = 0;
point[0][1] == point[1][1] ? y = 2 : point[0][1] == point[2][1] ? y = 1 : y = 0;
printf("%d %d", point[x][0], point[y][1]);
}단순히 x, y 값을 비교해서 1번만 나온 x값과 y값으로 답을 구했다.
문제를 풀고 나서 다른 사람 풀이를 보니 XOR연산(^)으로 풀었다.
구현 코드
#include<stdio.h>
int a,b,x,y;
int main(){
while(scanf("%d%d",&a,&b)==2)x^=a,y^=b;
printf("%d %d",x,y);
}
집합 관점에서 봤을 때, XOR 연산은 다음과 같이 표현 될 수 있다.
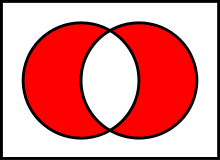
1. A⊕B의 벤 다이어그램
2. A⊕B⊕C의 벤 다이어그램
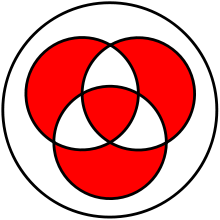
위 그림에서 보면, XOR 연산을 할 때, 다음과 같은 특징을 갖는다.
- 홀수번 합해지는 부분은 빨간색이다.
- 짝수번 합해지는 부분은 흰색이다.
XOR 연산의 특징
- true, false만을 갖는 집합 P = {p1, p2, p3, .... , pn}에서 p1 ⊕ p2 ⊕ .... ⊕ pn 합은 2로 모듈로한 값과 동일하다.
- 교환 법칙이 성립한다. p1 ⊕ p2 = p2 ⊕ p1
- 결합 법칙이 성립한다. (p1 ⊕ p2) ⊕ p3 = p1 ⊕ (p2 ⊕ p3)
따라서,
(A ⊕ B) ⊕ A = B
(A ⊕ B) ⊕ B = A
의 결과를 얻을 수 있고, 이 문제에서는 홀수번 등장한 x,y값이 답이 되므로 xor 연산을 사용해서 문제를 풀 수 있다.
References
728x90
반응형
'알고리즘 > 알고리즘 구현' 카테고리의 다른 글
| [BOJ 9663] N-Queen (0) | 2020.07.16 |
|---|---|
| [BOJ 2231] 분해합 , [BOJ 4673] 셀프 넘버 (0) | 2020.07.14 |
| [BOJ 1002] 터렛 (0) | 2020.07.11 |
| [BOJ 15552] 빠른 A+B (0) | 2020.07.07 |
| [BOJ 1799] 비숍 (2) | 2020.06.26 |

