Goal
- 그래프 순회(탐색)에 대한 이해
- BFS, DFS에 대한 이해
- BFS, DFS를 구현할 수 있다
그래프 순회(Graph Traversal/Search)
그래프에의 임의의 한 정점에서 시작하여 모든 정점들을 한 번씩 방문하는 작업
보통 그래프 순회, 그래프 탐색을 동일한 의미로 사용하므로 편의상 그래프 탐색이라 칭하겠다.
(단어 의미를 엄밀히 따지자면 그래프 순회가 좀 더 정확한 표현이다)
(참고)
Search vs Traversal
순회(Traversal)와 탐색(Search)이 동일한 의미로 사용 되기도 하는데, 굳이 구분하자면 다음과 같다.
- 탐색(Search) : index나 해싱 등의 방법으로 원하는 데이터를 빠르게 찾는 방법
- 순회(Traversal) : 특정 순회 알고리즘을 사용하여 모든 노드를 방문하는 방법
탐색(search)는 관심 대상은 그래프 안의 특정 값(노드)이다. 그 관심 대상을 빠르게 찾는 검이 탐색의 목적이다.
반면, 순회(traversal)는 특정 노드 뿐만이 아니라 모든 노드가 관심 대상이다. 즉, 그래프 자체가 순회의 관심 대상이다. 순회를 통해 특정 값을 찾는 것도 가능하고 그래프를 가공하는 것이 가능해진다.
그래프 탐색(순회)은 왜 중요할까? (개인적인 생각)
- 그래프 탐색은 모든 정점을 방문하기 때문에 탐색을 통해 그래프 특징을 알 수 있다.
- 또한, 방문하면서 checking, update 등과 같은 처리가 가능하기 때문에 그래프를 가공할 수 있다.
BFS, DFS와 같은 그래프 탐색 기법을 사용하면 스패닝 트리(Spanning Tree)를 구할 수 있다.
즉, 탐색을 통해 (그래프 -> Spanning Tree 또는 MST - Minimu Spanning Tree)로 만들수 있다. (이게 중요하다)
가중치 그래프를 따로 정리하면서 최소 신장 그래프에 대해서 설명할 것이므로 여기서는 '탐색을 통해 최소 신장 그래프를 얻을 수 있다' 정도만 알고 넘어가자
그래프 탐색 방법
대표적인 그래프 탐색(순회) 방법으로 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)이 있다.
깊이 우선 탐색 - DFS(Depth-first search)
자식 노드를 우선적으로 탐색하는 탐색 기법
= 아직 방문되지 않은 인접 노드(자식 노드)를 우선적으로 탐색
깊이 우선 탐색은 한쪽만 죽어라 파다가 더이상 팔 곳이 없으면 다시 돌아와서 다른 한쪽을 죽어라 파는 형식이다.
깊이 우선 탐색은 Stack을 통해 구현된다.
그렇기 때문에 DFS를 구현할 떄 stack이나 재귀 함수를 사용할 수 있다.
(재귀 함수를 사용하면 call stack을 사용하기 때문에 stack overflow를 조심해야 한다)
[깊이 우선 탐색, DFS]
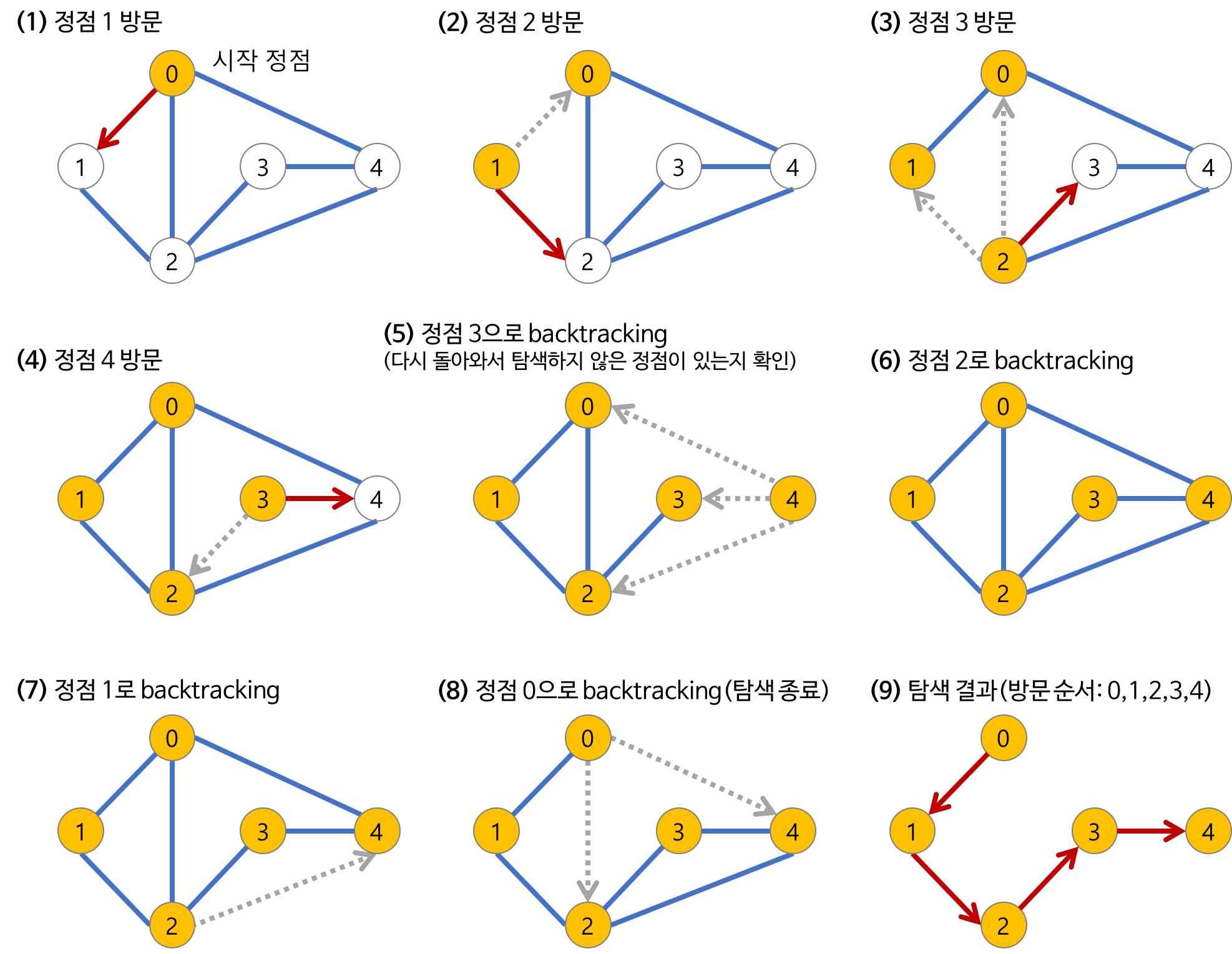


시간 복잡도
인접 리스트 : O(V+E)
인접 행렬 : O(V^2)
DFS의 활용
Spanning Tree, Connected Component, Strongly Connected Component
너비 우선 탐색 - BFS(Breadth-first search)
형제 노드를 우선적으로 탐색하는 탐색 기법. (레벨 순회(level-order traversal)라고도 한다)
= 아직 방문되지 않은 이전 노드(부모 노드)의 인접 노드(현재 노드의 형제 노드)를 우선적으로 탐색
보통 너비 우선 탐색은 Queue를 통해 구현된다.
[너비 우선 탐색, BFS]
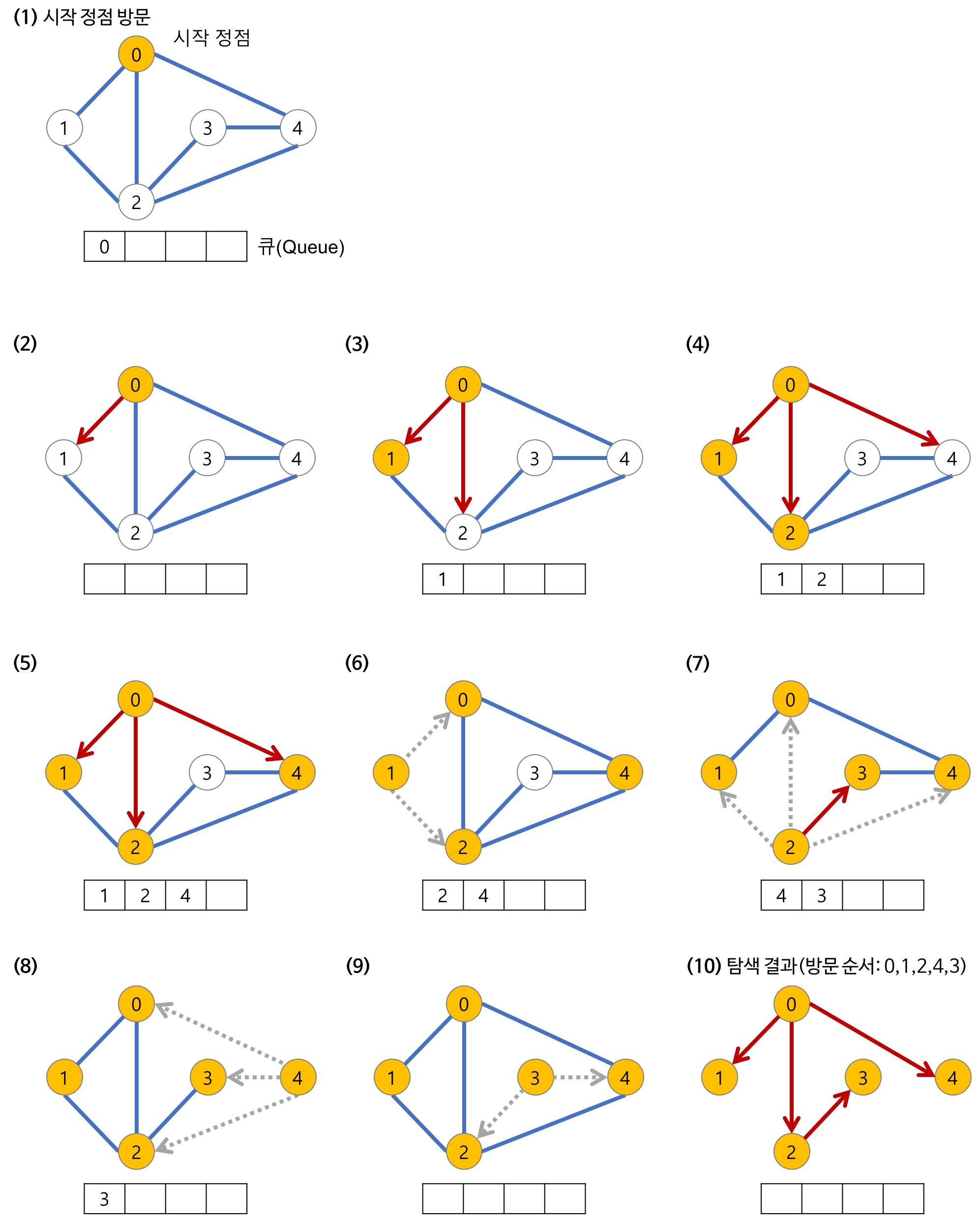


시간 복잡도
인접 리스트 : O(V+E)
인접 행렬 : O(V^2)
BFS의 활용
최단 경로 탐색, Spanning Tree, Connected Component, Strongly Connected Component
최단 경로 탐색에서 DFS가 아닌 BFS가 선호되는 이유
BFS를 사용하면 매 탐색마다 휴리스틱 값을 찾아서 가장 최선의 휴리스틱 값의 노드로 확장이 가능하기 때문에 DFS대신 BFS가 최단 경로 탐색에 사용된다.
*휴리스틱(heuristic)
휴리스틱(heuristics) 또는 발견법(發見法)이란 불충분한 시간이나 정보로 인하여 합리적인 판단을 할 수 없거나, 체계적이면서 합리적인 판단이 굳이 필요하지 않은 상황에서 사람들이 빠르게 사용할 수 있게 보다 용이하게 구성된 간편추론의 방법이다.
=> '대충 어림 짐작하기'라는 의미로 생각하면 된다.
ex) A* 알고리즘에서 거리 계산할 때, 정확한 값이 아닌 휴리스틱 추정값을 사용해서 구현한다.
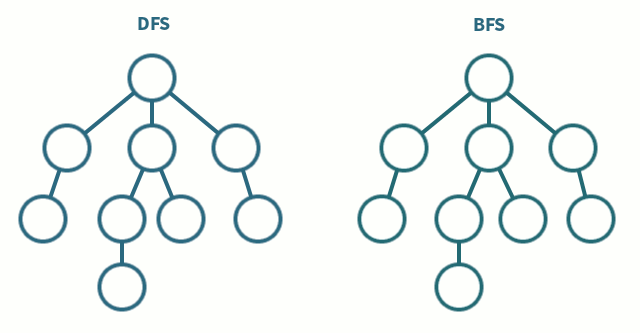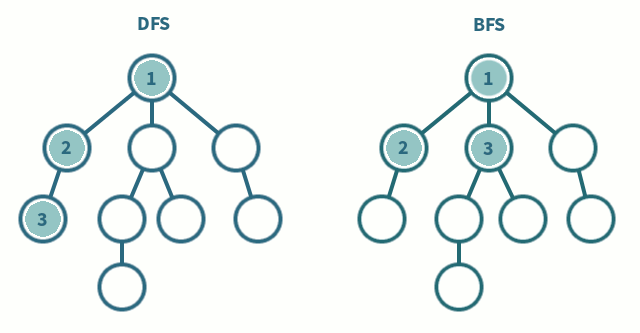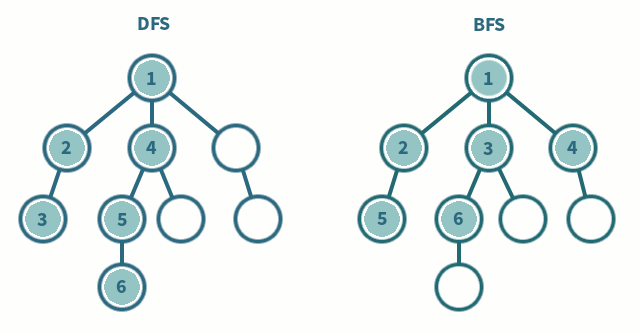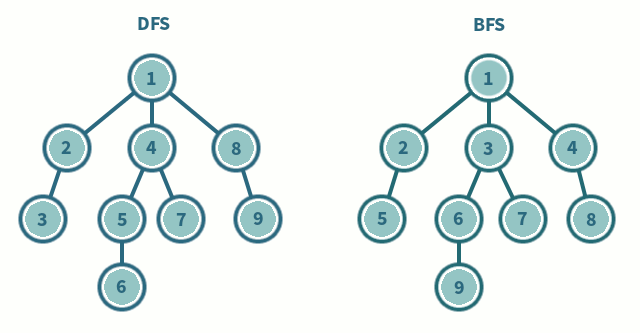
다음은 DFS, BFS를 구현한 함수이다. (BOJ 1206문제)
void DFS(int start)
{
visit[start] = true;
for (int i = 1; i <= N; i++)
{
if (false == visit[i] && true == edge[start][i])
{
DFS(i);
}
}
}
void BFS(int start)
{
std::queue<int> q;
q.push(start);
visit[start] = true;
while (false == q.empty())
{
int vertex = q.front();
printf("%d ", vertex);
q.pop();
for (int i = 1; i <= N; i++)
{
if (false == visit[i] && true == edge[vertex][i])
{
q.push(i);
visit[i] = true;
}
}
}
}
[참고]
https://gmlwjd9405.github.io/2018/08/15/algorithm-bfs.html
'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| Kruskal 알고리즘 (0) | 2020.07.01 |
|---|---|
| Union-Find (0) | 2020.07.01 |
| 반복과 재귀 (0) | 2020.06.30 |
| 코딩 테스트 입문 (with C++) (0) | 2020.06.11 |
| 알고리즘 문제 풀이를 위한 C++ 개발 환경 (0) | 2020.06.10 |

